Регресія

Значення змінної може варіюватися, мінятися від одного спостереження до іншого.  Наприклад, для різних індивідів з різними рисами характеру темпи коливання рівня ендорфінів у мозку будуть різними. Температура погоди за вікном буде різною на різних проміжках часу (вдень та вночі). 

При роботі зі статистичними моделями дослідники намагаються виявити загальні тенденції та закономірності змін між досліджуваними величинами.

Для цього виділяють так звану залежну та незалежну змінну — тобто робиться припущення, що значення однієї змінної змінюється внаслідок коливань значень деякої іншої змінної. Наприклад, рівень споживання природного газу домогосподарствами змінюється залежно від температури повітря в Україні. Тут температура повітря — незалежна змінна, а рівень споживання природного газу — залежна змінна.

Регресійний аналіз допомагає зрозуміти, яким чином типове значення залежної змінної змінюється внаслідок змін значень незалежної змінної (у той час, як інші незалежні змінні зафіксовано).

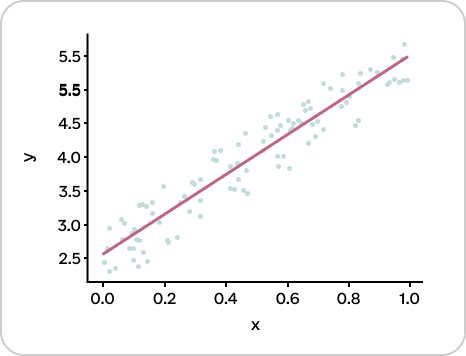
Результатом довільного регресійного аналізу є побудова рівняння (функції залежності)  між залежною та незалежною змінною. Наприклад, у випадку лінійної регресії рівняння функції залежності матиме вигляд 

y = 15 + 3x

Регресійна модель дозволяє передбачати та пояснювати фактори. 

• Передбачення дає нам уявлення, як буде поводити себе залежна змінна, якщо незалежна змінна буде приймати певні значення. Тобто, маючи x, можна спрогнозувати y (адже нам відоме рівняння регресії, побудоване на основі масиву спостережень). 

• Пояснення факторів — це можливість зрозуміти, наскільки y залежить від x, тобто який внесок робить незалежна змінна у залежну. Але важливо пам’ятати, що в такому випадку ми говоримо лише про лінійний зв’язок.